ایکسل میں MINVERSE | MINVERSE فنکشن کا استعمال کرتے ہوئے الٹا میٹرکس حاصل کریں
ایکسل میں MINVERSE فنکشن
ایکسل میں MINVERSE کا مطلب "میٹرکس الٹا" ہے۔ یہ بلٹ ان ایکسل فنکشن دیئے گئے میٹرکس کو اتنے ہی ارایوں کے ساتھ الٹا میٹرکس میں تبدیل کرتا ہے۔
"الٹا میٹرکس" کے بارے میں بات کرنے سے کسی کو یہ سمجھنے کی ضرورت ہوتی ہے کہ بالکل "الٹا میٹرکس" کیا ہے۔
الٹا میٹرکس: کسی عدد کے تکرار کو "الٹا میٹرکس" کہا جاتا ہے۔ مثال کے طور پر ، نمبر 5 کے ل we ، ہم باہمی طور پر تحریر لکھ سکتے ہیں
لہذا ، اس مساوات کو استعمال کرکے الٹا میٹرکس اسی منطق میں لکھا جاسکتا ہے "A-1" اور مذکورہ نمبر کو لکھا جاسکتا ہے 5-1 اس کے ساتھ ساتھ. جب ہم کسی تعداد کو اس کے باہمی لحاظ سے ضرب دیتے ہیں تو ہم ہمیشہ حاصل کرتے ہیں 1 نتیجے کے طور پر. مثال کے طور پر ، نمبر 5 اس کے باہمی 1/5 سے ضرب ہے ہم 13 کے نتیجے میں حاصل کرتے ہیں

اسی طرح ، جب ہم کسی میٹرکس کو اس کے الٹا سے ضرب دیتے ہیں تو ہمیں شناخت میٹرکس یعنی "I" مل جاتی ہے۔ ذیل میں شناختی میٹرکس کا مساوات ہے۔
A * A-1 = I
جب ہم ایکسل میں الٹا میٹرکس کے بارے میں بات کرتے ہیں تو ہمیں شناختی میٹرکس کو بھی دیکھنے کی ضرورت ہوتی ہے۔ شناختی میٹرکس کے ساتھ ، قطار اور کالم کی تمام تعداد مساوی تعداد میں ہوتی ہیں ، اخترن کے ساتھ ہمیں ایک قیمت مل جاتی ہے اور اخترن کے علاوہ باقی سب کچھ صفر کے برابر ہوجاتا ہے۔
تو ، شناختی میٹرکس ہمیشہ کی شکل میں رہے گا “2 * 2, 3 * 3, 4 * 4” اس طرح.
ایک بار جب میٹرکس الٹا ہے تو ہم ایکسل میں MMULT فنکشن کا استعمال کرکے الٹا ہے یا نہیں اس کی جانچ کر سکتے ہیں اور ہمیں ایک شناختی میٹرکس مل جائے گا اور ایسا لگتا ہے۔

ٹھیک ہے ، اب ان چیزوں کو ایکسل کے ساتھ آزمائیں۔
MINVERSE ایکسل فنکشن کو استعمال کرنے کی مثال
آپ یہاں ایکسل ٹیمپلیٹ میں MINVERSE - ایکسل ٹیمپلیٹ میں MINVERSE ڈاؤن لوڈ کرسکتے ہیںمثال کے طور پر ، نیچے 3 * 3 میٹرکس پر ایک نظر ڈالیں۔

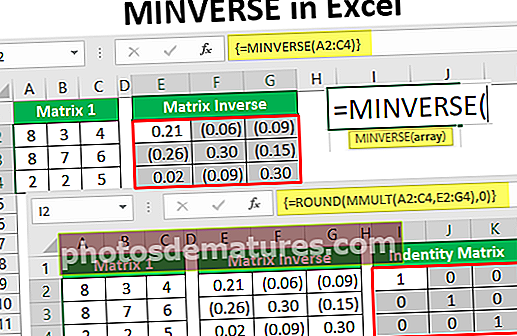
- ہمارے پاس A2 سے C4 تک میٹرکس نمبر ہیں ، تاکہ اس میٹرکس کو الٹ کر اوپر دی جدول کے آگے ایک جیسی ٹیبل بنائی جاسکے لیکن ایک جیسے اقدار کو برقرار نہ رکھیں اور فیلڈ کو خالی نہ رکھیں۔

- ای 2 سے جی 4 کی حد میں ہم میٹرکس کا الٹا پیدا کرنے جارہے ہیں۔ E2 سے G4 تک سیلوں کی حد منتخب کریں۔

- اب خلیوں کی منتخب کردہ رینج میں ایکسل MINVERSE فنکشن کو کھولیں۔

- MINVERSE فنکشن کی پہلی دلیل ہے سرنی یعنی یہ میٹرکس اقدار کی حد کے سوا کچھ نہیں ہے جسے ہم الٹا کرنے کی کوشش کر رہے ہیں ، لہذا ہماری 3 * 3 میٹرکس اقدار A2 سے C4 کی حد میں ہیں۔

اس سے پہلے کہ ہم فارمولا بند کردیں ایک چیز جو ہمیں دھیان میں رکھنی ہوگی وہ ہے "MINVERSE" ایک صف ہے لہذا ہمیں "CSE" کی چابیاں استعمال کرکے فارمولا کو بند کرنے کی ضرورت ہے۔
نوٹ: سی ایس ای کا مطلب ہے "Ctrl + شفٹ + داخل کریں". لہذا تمام صفوں کے فارمولے صرف ان چابیاں کے ساتھ بند کردیئے گئے ہیں۔- لہذا ، "Ctrl + شفٹ" کلید کو ایک ساتھ تھام کر ENTER کی کو دباکر فارمولا بند کردیں۔

جیسا کہ آپ دیکھ سکتے ہیں کہ MINVERSE فنکشن کا استعمال کرکے ہمیں "الٹا میٹرکس" ملا ہے۔ چونکہ یہ ایک صف کا فارمولا ہے ہم گھوبگھرالی خطوط دیکھ سکتے ہیں ({}) سرنی فارمولے کے آغاز اور اختتام پر۔
اب ہم جانچ کر سکتے ہیں کہ MMULT فنکشن کا استعمال کرکے یہ میٹرکس الٹا ہے یا نہیں۔ MMULT فنکشن کا مطلب "میٹرکس ضرب" ہے۔
- اب ایک اور شناختی میٹرکس بنانے کے لئے سیلوں کی حد منتخب کریں ، لہذا 3 * 3 میٹرکس کا علاقہ منتخب کریں۔

- اب خلیوں کی منتخب کردہ رینج کے لئے MMULT فنکشن کو کھولیں۔

- کے لئے سرنی 1 MMULT فنکشن کی دلیل A2 سے C4 تک "میٹرکس 1" کا انتخاب کریں۔

- کے لئے سرنی 2 MMULT فنکشن کی دلیل E2 سے G4 تک سیلوں کی "الٹا میٹرکس" کی حد منتخب کریں۔

- MMULT بھی ایک سرنی کام ہے ، لہذا سرنی فنکشن میں تبدیل کرنے کے لئے "CSE" کی چابیاں استعمال کرکے فارمولہ بند کردیں۔

- اس نتیجہ نے ہمیں اعشاریہ نتائج دیئے ہیں ، لہذا ایک درست "شناختی میٹرکس" حاصل کرنے کے لئے سرنی فعل کے اندر گول فنکشن کا استعمال کریں۔

اب ہمیں ایک "شناختی میٹرکس" مل گیا ہے جہاں ہمارے پاس اخترن ویلیو کی حیثیت سے 1 ہے۔ اس طرح ، ہم MINVERSE فنکشن کو میٹرکس اور MMULT کو الٹا کرنے کے ل use چیک کرسکتے ہیں کہ آیا یہ الٹ ہے یا نہیں۔
یاد رکھنے والی چیزیں
- MINVERSE فنکشن ایک وقت میں صرف ایک میٹرکس قبول کرسکتا ہے۔
- یہ ایکسل میں ایک صف فعل ہے لہذا فارمولہ بند کرنے کے لئے "CSE" کی چابیاں استعمال کریں۔
- جب میٹرکس الٹا ہوتا ہے تو ہم MMULT فنکشن کا استعمال کرکے شناختی میٹرکس تلاش کرسکتے ہیں جہاں ہمیں اصل میٹرکس کو الٹا میٹرکس کے ساتھ ضرب کرنے کی ضرورت ہوتی ہے۔