پیئرسن صلح کا کوفی (فارمولا ، مثال) | پیئرسن آر کا حساب لگائیں
پیئرسن صلح صفائی کی گہری تعریف
پیئرسن کا ارتباط قابلیت ، جسے پیئرسن آر شماریاتی ٹیسٹ بھی کہا جاتا ہے ، مختلف متغیرات اور ان کے تعلقات کے مابین طاقت کی پیمائش کرتا ہے۔ جب بھی کوئی اعدادوشمار ٹیسٹ دونوں متغیر کے مابین کرایا جاتا ہے ، تب یہ تجزیہ کرنے والے شخص کے لئے یہ جاننے کے لئے کہ آپس کے قابلیت کی قیمت کا حساب لگانا ہمیشہ ایک اچھا خیال ہے۔
پیئرسن کے ارتباط کے گتانک -1 اور 1 کے درمیان ایک قیمت واپس کرتا ہے۔ ارتباط کے قابلیت کی تشریح اس طرح ہے:
- اگر ارتباط کا قابلیت -1 ہے ، تو یہ مضبوط منفی تعلق کی نشاندہی کرتا ہے۔ یہ متغیر کے درمیان ایک کامل منفی تعلقات کا مطلب ہے۔
- اگر ارتباط کی گنجائش 0 ہے تو ، اس سے کوئی رشتہ نہیں ہوتا ہے۔
- اگر ارتباط کا قابلیت 1 ہے ، تو یہ ایک مضبوط مثبت رشتہ کی نشاندہی کرتا ہے۔ یہ متغیر کے درمیان ایک بہترین مثبت تعلقات کا مطلب ہے۔
ارتباط کے قابلیت کی ایک اعلی مطلق قیمت متغیر کے مابین مضبوط تعلقات کی نشاندہی کرتی ہے۔ اس طرح ، 0.78 کا ایک باہمی تعلق استقبال ایک مضبوط مثبت ارتباط کی نشاندہی کرتا ہے جبکہ 0.36 کہنے کی قدر کے مقابلے میں۔ اسی طرح -0.40 کے ارتباط کے قابلیت کے مقابلے میں -0.87 کا باہمی تعلق استقامت ایک مضبوط منفی ارتباط کی نشاندہی کرتا ہے۔

دوسرے لفظوں میں ، اگر قیمت مثبت حد میں ہے ، تو پھر یہ ظاہر ہوتا ہے کہ متغیر کے مابین تعلقات مثبت طور پر باہمی تعلق رکھتے ہیں ، اور دونوں اقدار ایک ساتھ مل کر گھٹ جاتے ہیں یا بڑھتے ہیں۔ دوسری طرف ، اگر قیمت منفی رینج میں ہے ، تو یہ ظاہر کرتا ہے کہ متغیر کے مابین کا تعلق منفی طور پر باہمی تعلق رکھتا ہے ، اور دونوں اقدار متضاد سمت میں جائیں گی۔
پیئرسن کا ارتباط کوفیف فارمولا
پیئرسن کا ارتباط کوفیف فارمولا مندرجہ ذیل ہے ،

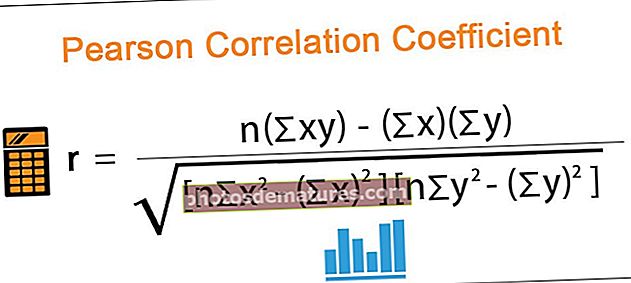
کہاں،
- r = پیئرسن گتانک
- n = اسٹاک کے جوڑے کی تعداد
- جوڑا = اسٹاک کی مصنوعات کا مجموعہ
- scorex = ایکس سکور کا مجموعہ
- =y = y اسکورز کا مجموعہ
- ∑x2 = مربع ایکس سکور کا مجموعہ
- ∑y2 = مربع y اسکورز کا مجموعہ
وضاحت
مرحلہ نمبر 1: متغیرات کے جوڑے کی تعداد معلوم کریں ، جو n کے ذریعہ ظاہر ہوتا ہے۔ آئیے فرض کریں کہ x 3 متغیر پر مشتمل ہے - 6 ، 8 ، 10۔ آئیے ہم فرض کریں کہ y 3 ، متغیر 12 ، 10 ، 20 پر مشتمل ہے۔
مرحلہ 2: متغیرات کو دو کالموں میں درج کریں۔

مرحلہ 3: تیسرے کالم میں x اور y کی مصنوع کا پتہ لگائیں۔

مرحلہ 4: تمام ایکس متغیرات اور تمام y متغیرات کی قدروں کا مجموعہ معلوم کریں۔ نتائج کو پہلے اور دوسرے کالم کے نیچے لکھیں۔ تیسرے کالم میں x * y کی رقم لکھیں۔

مرحلہ 5: چوتھے اور 5 ویں کالموں میں x2 اور y2 اور ان کے مجموعے کالم کے نچلے حصے میں تلاش کریں۔

مرحلہ 6: فارمولا میں مذکورہ اقدار داخل کریں اور اسے حل کریں۔
r = 3 * 352-24 * 42 / √ (3 * 200-242) * (3 * 644-422)
= 0.7559
پیئرسن کے ارتباط کوفیفٹی آر کی مثال
آپ یہ پیئرسن قرآلیشن کوفیفٹی ایکسل ٹیمپلیٹ ڈاؤن لوڈ کرسکتے ہیںمثال 1
اس مثال میں پیئرسن آر کی قیمت کے حساب کتاب کے لئے ذیل میں دیئے گئے 6 افراد کی عمر اور مختلف وزن رکھنے والے افراد کی جدول میں درج ذیل تفصیلات کی مدد سے

حل:
پیئرسن صلح صفائی کے حساب کتاب کے ل For ، ہم پہلے درج ذیل اقدار کا حساب لگائیں گے ،

یہاں لوگوں کی کل تعداد 6 ہے ، n = 6
اب پیئرسن آر کا حساب کتاب درج ذیل ہے ،

- r = (n (∑xy) - (∑x) (∑y)) / (√ [n ∑x2- (∑x) 2] [n ∑y2– ()y) 2)
- r = (6 * (13937) - (202) (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
- r = (6 * (13937) - (202) * (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
- r = (83622- 82618) / (√ [43680 -40804] * [170190- 167281)
- r = 1004 / (√ [2876] * [2909)
- r = 1004 / (6 8366284)
- r = 1004 / 2892.452938
- r = 0.35
اس طرح پیئرسن ارتباط کے گتانک کی قدر ہے 0.35
مثال # 2
یہاں 2 اسٹاک ہیں۔ A اور B. خاص دنوں میں ان کے حصص کی قیمتیں درج ذیل ہیں۔

مندرجہ بالا اعداد و شمار سے پیئرسن کا ارتباط کی گنجائش معلوم کریں۔
حل:
پہلے ، ہم درج ذیل اقدار کا حساب لگائیں گے۔

پیئرسن کوفیفی کا حساب کتاب اس طرح ہے ،

- r = (5*1935-266*37)/((5*14298-(266)^2)*(5*283-(37)^2))^0.5
- = -0.9088
لہذا دونوں اسٹاک کے مابین پیئرسن کا ارتباط قابلیت -0.9088 ہے۔
فوائد
- اس سے یہ جاننے میں مدد ملتی ہے کہ دونوں متغیر کے مابین کتنا مضبوط تعلق ہے۔ دونوں متغیر کے درمیان نہ صرف آپ کی موجودگی یا باہمی ربط کی عدم موجودگی کا اشارہ پیئرسن کوریلیشن کوففیٹ کا استعمال کرتے ہوئے کیا گیا ہے بلکہ اس سے یہ بھی طے ہوتا ہے کہ ان متغیروں کے آپس میں کیا تعلق ہے۔
- اس طریقہ کار کو استعمال کرتے ہوئے ، کوئی شخص باہمی تعلق کی سمت کا پتہ لگا سکتا ہے یعنی دو متغیر کے مابین باہمی ربط منفی ہے یا مثبت۔
نقصانات
- انحصار متغیرات اور آزاد متغیرات کے مابین فرق بتانے کے لئے پیئرسن کوریلیشن کوفیفٹ آر کافی نہیں ہے کیونکہ متغیر کے مابین کورلیشن قابلیت متوازی ہے۔ مثال کے طور پر ، اگر کوئی شخص اعلی تناؤ اور بلڈ پریشر کے مابین ارتباط کو جاننے کی کوشش کر رہا ہے ، تو پھر کسی کو اس ارتباط کی اعلی قیمت معلوم ہوسکتی ہے جس سے یہ ظاہر ہوتا ہے کہ ہائی تناؤ بلڈ پریشر کا سبب بنتا ہے۔ اب اگر متغیر کے ارد گرد تبدیل کر دیا گیا ہے تو ، اس صورت میں ، نتیجہ بھی وہی ہوگا جو ظاہر کرتا ہے کہ دباؤ بلڈ پریشر کی وجہ سے ہوتا ہے جس کا کوئی مطلب نہیں ہے۔ لہذا ، محقق کو ان اعداد و شمار سے آگاہ ہونا چاہئے جو وہ تجزیہ کرنے کے لئے استعمال کررہے ہیں۔
- اس طریقہ کار کو استعمال کرنے سے کوئی بھی لائن کی ڈھلوان کے بارے میں معلومات حاصل نہیں کرسکتا کیونکہ اس میں صرف یہ بتایا گیا ہے کہ آیا دونوں متغیر کے درمیان کوئی رشتہ موجود ہے یا نہیں۔
- اس بات کا امکان ہے کہ ہم جنس اعداد و شمار کے معاملے میں پیئرسن صلح صفائی کی غلط تشریح کی جاسکتی ہے۔
- جب حساب کے دیگر طریقوں سے موازنہ کیا جائے تو ، اس طریقے کو نتائج تک پہنچنے میں زیادہ وقت لگتا ہے۔
اہم نکات
- اقدار قدر +1 سے لے کر قیمت -1 تک کی ہوسکتی ہیں ، جہاں +1 غور کیے جانے والے متغیر کے مابین کامل مثبت تعلقات کی نشاندہی کرتا ہے ، -1 متغیر کے مابین کامل منفی تعلق کی نشاندہی کرتا ہے ، اور 0 قدر سے ظاہر ہوتا ہے کہ کوئی رشتہ نہیں ہے متغیر کے درمیان موجود ہے۔
- یہ متغیر کی پیمائش کے اکائی سے آزاد ہے۔ مثال کے طور پر ، اگر ایک متغیر کی پیمائش کی اکائی برسوں میں ہے جبکہ دوسرے متغیر کی پیمائش کی اکائی کلوگرام میں ہے ، تب بھی ، اس قابلیت کی قدر نہیں بدلی جاتی ہے۔
- متغیر کے مابین ارتباط کا گتانک متوازی ہے جس کا مطلب یہ ہے کہ Y اور X یا X اور Y کے درمیان باہمی ربط کی قدر ایک جیسی رہے گی۔
نتیجہ اخذ کرنا
پیئرسن کوریلیشن کوفیفٹی (Coelation Coeype) کی ایک قسم کا تعلق ہے جو دونوں متغیر کے مابین تعلقات کی نمائندگی کرتا ہے جو ایک ہی وقفہ یا ایک ہی تناسب کے پیمانے پر ماپا جاتا ہے۔ یہ دونوں مستقل متغیر کے مابین تعلقات کی مضبوطی کو ماپا کرتا ہے۔
اس میں نہ صرف دونوں متغیروں کے مابین ارتباط کی موجودگی یا عدم موجودگی کو بتایا گیا ہے بلکہ یہ اس بات کا بھی تعین کرتا ہے کہ ان متغیروں کے آپس میں کیا تعلق ہے۔ یہ متغیر کی پیمائش کے اکائی سے آزاد ہے جہاں ارتباط کے قابلیت کی قدر +1 سے قدر -1 تک ہوسکتی ہے۔ تاہم ، انحصار متغیر اور آزاد متغیر کے مابین فرق بتانا کافی نہیں ہے۔