کوارٹائل انحراف (فارمولا) | مثال کے ساتھ مرحلہ وار حساب کتاب
کوارٹائل انحراف کیا ہے؟
کوارٹائل انحراف تعدد کی تقسیم میں پہلے چوتھائی اور تیسرے چوتھائی کے مابین فرق پر مبنی ہے اور فرق کو بین الکاہلی حد کے نام سے بھی جانا جاتا ہے ، دو کو تقسیم کردہ فرق کو کوٹائلٹ انحراف یا نیم انٹرکویٹریٹ حد کے نام سے جانا جاتا ہے۔
جب کوئی تیسری چوتھائی اور ایک آسان تقسیم یا تعدد کی تقسیم کے پہلے چوتھائی کے درمیان فرق یا فرق کا نصف لیتا ہے تو چوتھائی انحراف ہوتا ہے۔
فارمولا
کوارٹائل انحراف (Q.D.) فارمولہ پھیلاؤ کو ماپنے کے ل statistics اعدادوشمار میں یا دوسرے الفاظ میں بازی کی پیمائش کرنے کے لئے استعمال ہوتا ہے۔ اسے سیمی انٹر کوارٹائل رینج بھی کہا جاسکتا ہے۔
Q.D. = کیو 3 - کیو 1/2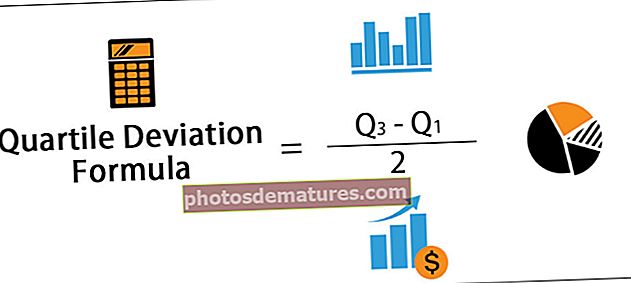
- اس فارمولے میں حساب کتاب میں Q3 اور Q1 شامل ہیں جو بالترتیب 25٪ ہے اور 25٪ ڈیٹا کو بالترتیب کم کرتا ہے اور جب ان دونوں کے درمیان فرق لیا جاتا ہے اور جب یہ تعداد آدھی ہوجاتی ہے تو پھر یہ پھیلاؤ یا بازی کے اقدامات فراہم کرتا ہے۔
- لہذا ، چوتھائی انحراف کا حساب لگانے کے لئے ، آپ کو پہلے Q1 تلاش کرنا ہوگا پھر دوسرا مرحلہ Q3 تلاش کرنا ہے اور پھر دونوں میں فرق لینا ہے اور آخری قدم 2 سے تقسیم کرنا ہے۔
- کھلی ہوئی اعداد و شمار کے لئے بازی کا یہ ایک بہترین طریقہ ہے۔
مثالیں
آپ کوارٹائل انحراف فارمولہ ایکسل سانچہ یہاں ڈاؤن لوڈ کرسکتے ہیںمثال # 1
درج ذیل نمبروں کے ایک اعداد و شمار کے سیٹ پر غور کریں: 22 ، 12 ، 14 ، 7 ، 18 ، 16 ، 11 ، 15 ، 12. آپ کو کوآرٹیلی انحراف کا حساب لگانا ضروری ہے۔
حل:
پہلے ، ہمیں Q3 اور Q1 تلاش کرنے اور کسی بھی نقول سے بچنے کے ل as چڑھتے ترتیب میں ڈیٹا کا بندوبست کرنے کی ضرورت ہے۔
7, 11, 12, 13, 14, 15, 16, 18, 22
کیو 1 کا حساب کتاب مندرجہ ذیل طور پر کیا جاسکتا ہے ،
Q1 = ¼ (9 + 1)
=¼ (10)
سوال 1=2.5 ٹرم
کیو 3 کا حساب کتاب مندرجہ ذیل طور پر کیا جاسکتا ہے ،
Q3 = ¾ (9 + 1)
=¾ (10)
س 3= 7.5 ٹرم
چوتھائی انحراف کا حساب کتاب مندرجہ ذیل طور پر کیا جاسکتا ہے ،
- کیو 1 دوسرا اوسطا ہے جو 11 ہے اور یہ تیسری اور چوتھی اور 0.5 کے درمیان فرق کی پیداوار کو جوڑتا ہے جو (12-11) * 0.5 = 11.50 ہے۔
- Q3 ساتویں اصطلاح اور 0.5 کی مصنوع ہے اور 8 ویں اور ساتویں اصطلاح کے درمیان فرق ہے جو (18-16) * 0.5 ہے اور نتیجہ 16 + 1 = 17 ہے۔
Q.D. = کیو 3 - کیو 1/2
چوتھائی انحراف کے فارمولے کا استعمال کرتے ہوئے ، ہمارے پاس (17-11.50) / 2 ہے
=5.5/2
Q.D.=2.75.
مثال # 2
ہیری لمیٹڈ ایک ٹیکسٹائل بنانے والا ہے اور انعام کے ڈھانچے پر کام کر رہا ہے۔ انتظامیہ ایک نیا اقدام شروع کرنے کے لئے بات چیت میں ہے ، لیکن وہ پہلے جاننا چاہتے ہیں کہ ان کی پیداوار کتنی پھیل رہی ہے۔
انتظامیہ نے پچھلے 10 دن (اوسط) ملازم کے لئے اپنے اوسط یومیہ پیداوار کا ڈیٹا اکٹھا کیا ہے۔
155, 169, 188, 150, 177, 145, 140, 190, 175, 156.
منتشر کو تلاش کرنے میں انتظامیہ کی مدد کے لئے کوآرٹائل انحراف کا فارمولا استعمال کریں۔
حل:
یہاں مشاہدات کی تعداد 10 ہے اور ہمارا پہلا مرحلہ یہ ہے کہ ڈیٹا ن کو چڑھتے ہوئے آرڈر کا بندوبست کیا جائے۔
140, 145, 150, 155, 156, 169, 175, 177, 188, 190
کیو 1 کا حساب کتاب مندرجہ ذیل طور پر کیا جاسکتا ہے ،
Q1 = ¼ (n + 1) th اصطلاح
=¼ (10+1)
=¼ (11)
سوال 1= 2.75 واں میعاد
کیو 3 کا حساب کتاب مندرجہ ذیل طور پر کیا جاسکتا ہے ،
Q3 = ¾ (n + 1) th اصطلاح
=¾ (11)
س 3= 8.25 میعاد
چوتھائی انحراف کا حساب کتاب مندرجہ ذیل طور پر کیا جاسکتا ہے ،
- دوسری اصطلاح 145 ہے اور اب اس نے 0.75 * (150 - 145) میں اضافہ کیا جو 3.75 ہے اور نتیجہ 148.75 ہے۔
- آٹھویں اصطلاح 177 ہے اور اب اس نے 0.25 * (188 - 177) میں اضافہ کیا ہے جو 2.75 ہے اور نتیجہ 179.75 ہے۔
Q.D. = کیو 3 - کیو 1/2
چوتھائی انحراف کے فارمولے کا استعمال کرتے ہوئے ، ہمارے پاس (179.75-148.75) / 2 ہے
=31/2
Q.D.=15.50.
مثال # 3
ریان کی بین الاقوامی اکیڈمی یہ تجزیہ کرنا چاہتی ہے کہ ان کے طلبا کے کتنے فیصد اسکور نمبر پھیلا رہے ہیں۔
ڈیٹا 25 طلباء کا ہے۔

کوآرٹائل انحراف کے فارمولے کو٪ نمبروں میں بازی معلوم کرنے کے لئے استعمال کریں۔
حل:
یہاں مشاہدات کی تعداد 25 ہے اور ہمارا پہلا قدم بڑھتے ہوئے ترتیب میں ڈیٹا کا بندوبست کرنا ہے۔

کیو 1 کا حساب کتاب مندرجہ ذیل طور پر کیا جاسکتا ہے ،
Q1 = ¼ (n + 1) th اصطلاح
=¼ (25+1)
=¼ (26)
سوال 1= 6.5 ویں میعاد
کیو 3 کا حساب کتاب مندرجہ ذیل طور پر کیا جاسکتا ہے ،
Q3 = ¾ (n + 1) th اصطلاح
=¾ (26)
س 3 = 19.50 میعاد
چوتھائی انحراف یا نیم انٹرکوئٹی رینج کا حساب کتاب مندرجہ ذیل طور پر کیا جاسکتا ہے ،
- چھٹی میعاد 154 ہے اور اب اس نے 0.50 * (156 - 154) میں اضافہ کیا ہے جو 1 ہے اور نتیجہ 155.00 ہے۔
- 19 ویں میعاد 177 ہے اور اب اس نے 0.50 * (177 - 177) میں اضافہ کیا ہے جو 0 ہے اور نتیجہ 177 ہے
Q.D. = کیو 3 - کیو 1/2
چوتھائی انحراف کے فارمولے کا استعمال کرتے ہوئے ، ہمارے پاس (177-155) / 2 ہے
=22/2
Q.D.= 11.
مثال # 4
آئیے اب عملی مثال I کے ایکسل ٹیمپلیٹ کے ذریعہ قیمت کا تعین کریں۔
حل:
چوتھائی انحراف کے حساب کتاب کے لئے درج ذیل اعداد و شمار کا استعمال کریں۔

کیو 1 کا حساب کتاب مندرجہ ذیل طور پر کیا جاسکتا ہے ،

سوال 1=148.75
کیو 3 کا حساب کتاب مندرجہ ذیل طور پر کیا جاسکتا ہے ،

س 3= 179.75
چوتھائی انحراف کا حساب کتاب مندرجہ ذیل طور پر کیا جاسکتا ہے ،

چوتھائی انحراف کے فارمولے کا استعمال کرتے ہوئے ، ہمارے پاس (179.75-148.75) / 2 ہے
Q.D. ہو جائے گا -

کیو ڈی = 15.50
متعلقہ اور استعمال
کوآرٹائل انحراف جو ایک نیم انٹرکوئٹی رینج کے نام سے بھی مشہور ہے۔ ایک بار پھر ، تیسری اور پہلی چوتھائی کے درمیان تغیرات کے فرق کو انٹرکویٹیل رینج کہا جاتا ہے۔ انٹرقیٹائل رینج اس حد تک دکھاتی ہے جس میں دیئے گئے ڈیٹاسیٹ کے مشاہدات یا قدروں کو وسط یا ان کی اوسط سے پھیلایا جاتا ہے۔ کوآرٹائل انحراف یا نیم انٹرقیٹیلی رینج ایسی صورت میں استعمال ہونے والی اکثریت ہے جہاں کوئی مشاہدات کی بازی یا دیئے گئے ڈیٹا سیٹس کے نمونوں کے بارے میں مطالعہ سیکھنا یا کہنا چاہتا ہے جو دیئے گئے سلسلہ کے مرکزی یا درمیانی حصے میں موجود ہے۔ یہ معاملہ عام طور پر کسی ایسی تقسیم میں ہوتا ہے جہاں اعداد و شمار یا سیریز اور اعدادوشمار کے دیئے گئے سیٹ کے سلسلے میں مرکزی اعضاء یا وسط میں اعداد و شمار یا مشاہدات شدت سے پڑے ہوتے ہیں اور تقسیم یا اقدار حدود کی طرف نہیں پڑتے ہیں اور اگر وہ جھوٹ بولتے ہیں تو وہ حساب کتاب کے لئے زیادہ اہمیت نہیں رکھتے ہیں۔