نمونہ سائز (تعریف ، فارمولا) | نمونے کے سائز کا حساب لگائیں
آبادی کا نمونہ سائز طے کرنے کا فارمولا
نمونہ سائز کا فارمولا کم سے کم نمونہ کے سائز کا حساب لگانے یا اس کا تعین کرنے میں مدد کرتا ہے جو اعتماد کی سطح اور غلطی کے مارجن کے ساتھ آبادی کا مناسب یا صحیح تناسب جاننے کے لئے ضروری ہے۔
اصطلاح "نمونہ" آبادی کے اس حصے سے مراد ہے جو آبادی کے بارے میں نقائص ہماری طرف متوجہ کرنے کے قابل بناتا ہے اور لہذا یہ ضروری ہے کہ نمونہ کی مقدار اتنی مناسب ہو کہ معنی خیز انکشاف کیا جاسکے۔ دوسرے الفاظ میں ، یہ کم سے کم سائز ہے جس میں غلطی اور اعتماد کی سطح کے مطلوبہ حاشیے کے ساتھ آبادی کے حقیقی تناسب کا اندازہ لگانے کے لئے درکار ہے۔ اسی طرح ، مناسب نمونے کے سائز کا تعین اعداد و شمار کے تجزیے میں بار بار آنے والی پریشانیوں میں سے ایک ہے۔ اس کی مساوات کو آبادی کے سائز ، عام تقسیم کی اہم قدر ، نمونہ تناسب ، اور غلطی کے مارجن کا استعمال کرکے حاصل کیا جاسکتا ہے۔
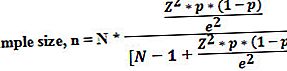

کہاں،
- N = آبادی کا سائز ،
- زیڈ = مطلوبہ اعتماد کی سطح پر معمول کی تقسیم کی اہم قدر ،
- p = نمونے کا تناسب ،
- ای = غلطی کا مارجن
نمونہ کے سائز کا حساب کتاب کیسے کریں؟ (قدم بہ قدم)
- مرحلہ نمبر 1: سب سے پہلے ، آبادی کا سائز طے کریں جو آپ کی آبادی میں الگ الگ اداروں کی کل تعداد ہے اور اسے این کے ذریعہ اشارہ کیا گیا ہے۔ [نوٹ: صورت میں ، آبادی کا سائز بہت زیادہ ہے لیکن صحیح تعداد معلوم نہیں ہے ، اس کے بعد 100،000 استعمال کریں کیونکہ نمونہ اس سے بڑی آبادی کیلئے سائز زیادہ تبدیل نہیں ہوتا۔]
- مرحلہ 2: اگلا ، مطلوبہ اعتماد کی سطح پر عام تقسیم کی اہم قدر کا تعین کریں۔ مثال کے طور پر ، 95 confidence اعتماد کی سطح پر اہم قیمت 1.96 ہے۔
- مرحلہ 3: اس کے بعد ، نمونے کے تناسب کا تعین کریں جو پچھلے سروے کے نتائج سے استعمال کیا جاسکتا ہے یا چھوٹا پائلٹ سروے چلا کر جمع کیا جاسکتا ہے۔ [نوٹ: اگر غیر یقینی بات ہے تو وہ ہمیشہ قدامت پسندانہ نقطہ نظر کے طور پر 0.5 استعمال کرسکتا ہے اور یہ نمونہ کا سب سے بڑا سائز دے گا۔]
- مرحلہ 4: اس کے بعد ، غلطی کے مارجن کا تعین کریں جس حد میں حقیقی آبادی کے جھوٹ بولنے کی توقع کی جارہی ہے. [نوٹ: غلطی کا مارجن چھوٹا ، زیادہ سے زیادہ صحت سے متعلق ہے لہذا عین مطابق جواب۔]
- مرحلہ 5: آخر میں ، نمونے کے سائز کی مساوات کو آبادی کے سائز (مرحلہ 1) ، مطلوبہ اعتماد کی سطح پر معمول کی تقسیم کی اہم قدر (مرحلہ 2) ، نمونہ تناسب (مرحلہ 3) اور غلطی کے مارجن (مرحلہ 4) کے ذریعہ حاصل کیا جاسکتا ہے۔ نیچے دکھایا گیا.
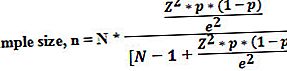
مثالیں
آپ یہ نمونہ سائز فارمولا ایکسل ٹیمپلیٹ ڈاؤن لوڈ کرسکتے ہیں - نمونہ سائز کا فارمولا ایکسل ٹیمپلیٹمثال # 1
آئیے ہم ایک خوردہ فروش کی مثال لیتے ہیں جو یہ جاننے میں دلچسپی رکھتا ہے کہ ان کے کتنے صارفین نے اپنی ویب سائٹ کو ایک خاص دن دیکھنے کے بعد ان سے ایک آئٹم خریدا۔ یہ بتاتے ہوئے کہ ان کی ویب سائٹ میں روزانہ اوسطا 10،000 آراء ہیں ، ان صارفین کے نمونہ کا اندازہ لگائیں جو انہیں 95٪ اعتماد کی سطح پر 5 margin غلطی کے مارجن کے ساتھ ماننا ہے۔
- وہ موجودہ تبادلوں کی شرح سے غیر یقینی ہیں۔
- وہ پچھلے سروے سے جانتے ہیں کہ تبادلوں کی شرح 5٪ ہے۔
دیئے گئے ،
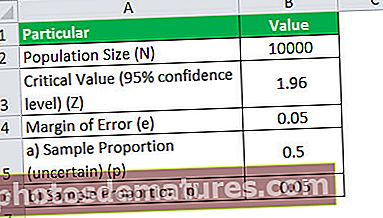
- آبادی کا سائز ، N = 10،000
- 95 confidence اعتماد کی سطح پر اہم قیمت ، زیڈ = 1.96
- غلطی کا مارجن ، e = 5٪ یا 0.05
1 - چونکہ موجودہ تبادلوں کی شرح معلوم نہیں ہے ، ہم آئیے پی = 0.5 مان لیں
لہذا ، فارمولے کا استعمال کرتے ہوئے نمونہ کے سائز کا حساب لگایا جاسکتا ہے ،
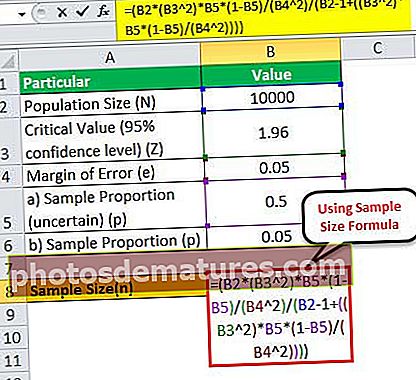
= (10,000 * (1.96 2)*0.5*(1-0.5)/(0.05 2)/(10000 – 1+((1.96 2)* 0.5*(1-0.5)/(0.05 2))))
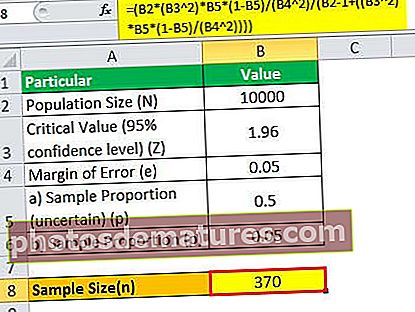
لہذا ، 370 گراہک معنی خیز اخذ کرنے کے ل adequate کافی ہوں گے۔
2 - موجودہ تبادلوں کی شرح p = 5٪ یا 0.05 ہے
لہذا ، نمونہ کے سائز کا حساب مندرجہ بالا فارمولے کا استعمال کرکے کیا جاسکتا ہے ،
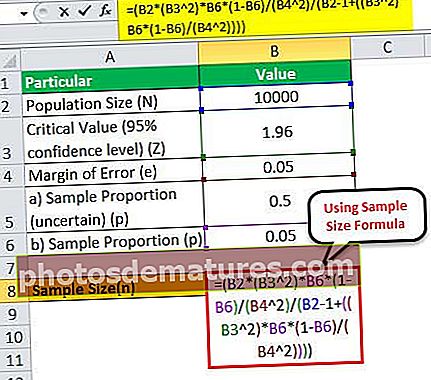
= (10,000 * (1.96 2)*0.05*(1-0.05)/(0.05 2)/(10000 – 1+((1.96 2)* 0.05*(1-0.05)/(0.05 2))))
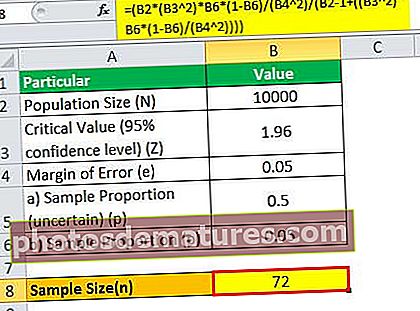
لہذا ، اس معاملے میں بامعنی تعبیر حاصل کرنے کے لئے 72 صارفین کا سائز کافی ہوگا۔
مثال # 2
آئیے مذکورہ بالا مثال کو لیں اور اس معاملے میں آئیے ہم یہ فرض کریں کہ آبادی کا سائز ، یعنی روزانہ کی ویب سائٹ کا نظارہ ، 100،000 اور 120،000 کے درمیان ہے ، لیکن پھر اس کی صحیح قدر معلوم نہیں ہوسکتی ہے۔ 5 of کی شرح تبادلہ کے ساتھ باقی اقدار ایک جیسی ہیں۔ 100،000 اور 120،000 دونوں کے لئے نمونے کے سائز کا حساب لگائیں۔
دیئے گئے ،
- نمونہ تناسب ، p = 0.05
- 95 confidence اعتماد کی سطح پر اہم قیمت ، زیڈ = 1.96
- غلطی کا مارجن ، e = 0.05
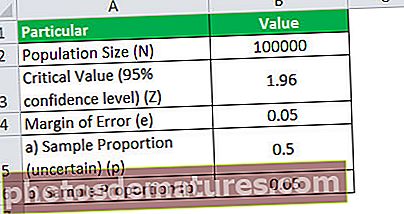
لہذا ، N = 100،000 کے لئے نمونے کے سائز کا حساب کتاب کیا جاسکتا ہے ،
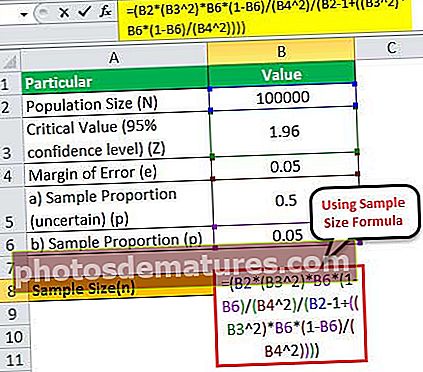
= (100000 * (1.96 2)*0.05*(1-0.05)/(0.05 2)/(100000 – 1+((1.96 2)* 0.05*(1-0.05)/(0.05 2))))
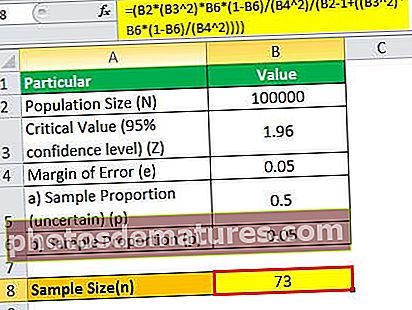
لہذا ، N = 120،000 کے لئے نمونے کے سائز کا حساب کتاب کیا جاسکتا ہے ،
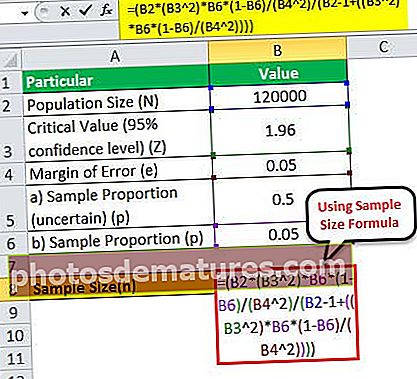
= (120000 * (1.96 2)*0.05*(1-0.05)/(0.05 2)/(120000 – 1+((1.96 2)* 0.05*(1-0.05)/(0.05 2))))
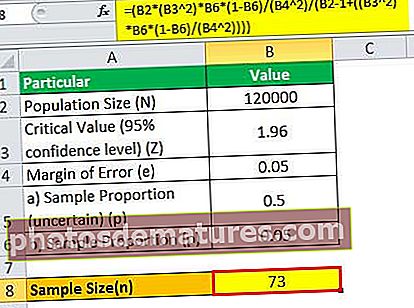
لہذا ، یہ ثابت ہوا کہ جیسے جیسے آبادی کا سائز بہت زیادہ بڑھ جاتا ہے ، یہ نمونے کے سائز کی گنتی میں غیر متعلق ہو جاتا ہے۔
متعلقہ اور استعمال
نمونے کے سائز کا حساب کتاب نمونے کے مناسب سائز کے تصور کو سمجھنے کے لئے ضروری ہے کیونکہ یہ تحقیق کے نتائج کی درستگی کے لئے استعمال ہوتا ہے۔ اگر یہ بہت چھوٹا ہے تو ، اس کے درست نتائج برآمد نہیں ہوں گے ، جبکہ ایک نمونہ بہت بڑا ہے تو یہ رقم اور وقت دونوں کا ضائع ہوسکتا ہے۔ اعدادوشمار کے مطابق ، اہم نمونہ سائز بنیادی طور پر مارکیٹ ریسرچ سروے ، صحت کی دیکھ بھال کے سروے ، اور تعلیم کے سروے کے لئے استعمال کیا جاتا ہے۔